Time-varying BIBO stability Analysis of Andrew Simper trapazoidal integrated SVF
Analysis by Ross Bencina [rossb@audiomulch.com]
The filter:
http://www.cytomic.com/files/dsp/SvfLinearTrapOptimised2.pdf
The stability anaysis follows the method given by Jean Laroche in:
Laroche, Jean. "On the Stability of Time-Varying Recursive Filters"
JAES Volume 55 Issue 6 pp. 460-471; June 2007
http://www.aes.org/e-lib/browse.cfm?elib=14168
This analysis was prepared using the following tools:
wxMaxima: http://sourceforge.net/projects/wxmaxima/
Wolfram Alpha: http://www.wolframalpha.com/
Desmos graphing calculator: https://www.desmos.com/calculator
INTRODUCTION
The purpose of this analysis is to show that the above referenced filter is stable even when time-varying parameters k and g are varied at audio rate.
You will need to read Laroche's paper for the background and the proofs of the results used here. I don't attempt to explain why the stability criteria are sufficient. Laroche gives a direct and easy to follow argument starting with the state-space representation of the filter.
I make no claim to know what I'm doing. I'm still learning to perform this kind of mathematical analysis. I'd appreciate feedback on my method or if I've made an error. I'm happy to answer questions by email or on the music-dsp mailing list.
TIME DOMAIN SCALAR FILTER ALGORITHM AS GIVEN BY ANDREW SIMPER
This is the time-domain, scalar implementation of the trapazoidal integrated SVF.
This was copied directly from Andrew Simper's .pdf above, with some minor syntax changes for Maxima.
We use these scalar equations to form the state transition matrix P in the next section.
We perform all analysis in terms of the filter parameters g (a function of cutoff frequency) and k (a function of resonance/damping).
Note that g>0 and 0 < k <= 2. This is important for the analysis.
We wish to show that the filter is time-varying BIBO stable for all valid values of g and k.
| (%i1) |
/*SVF "Final Algorithm" page 2-3. */ /* wc : %pi*cutoff/samplerate; g : tan(wc); k : 2-2*res; // k on (0,2) => 0=undamped */ /* declarations not really used at this stage */ declare(g,[real,scalar,constant]); assume( g >= 0 ); declare(k,[real,scalar,constant]); assume( k > 0 ); assume( k <= 2 ); /* state variables */ declare(ic1eq,[real,scalar]); declare(ic2eq,[real,scalar]); /* coefficients are functions of g and k */ a1 : 1/(1 + g*(g + k)); a2 : g*a1; a3 : g*a2; |
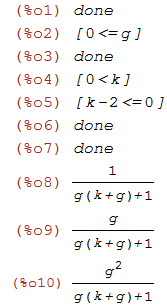
| (%i11) |
/* compute voltages for current timestep */ v3 : v0 - ic2eq; v1 : a1*ic1eq + a2*v3; v2 : ic2eq + a2*ic1eq + a3*v3; /* compute updated states. i've used _ to indicate the n+1 timestep */ ic1eq_ : 2*v1 - ic1eq; ic2eq_ : 2*v2 - ic2eq; /* compute outputs. it turns out the stability analysis only depends on the state transition matrix P derived from the statements above, but here are the output equations anyway: */ low : v2; band : v1; high : v0 - k*v1 - v2; notch : v0 - k*v1; |

So these are the expanded and simplified state update equations that compute the next filter states [ic1eq_,ic2eq_] from the current filter state [ic1eq,ic2eq], the input v0, and the parameters k and g.
| (%i20) | fullratsimp(ic1eq_); |
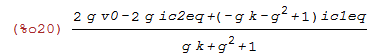
| (%i21) | fullratsimp(ic2eq_); |
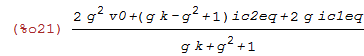
We use these expressions in the next section to derive the state transition matrix P used for the stability analysis.
STEP 1. DERIVE STATE TRANSITION MATRIX P FROM THE SCALAR IMPLEMENTATION ABOVE
Laroche gives (in sec 1.2) a state-space representation of a time varying filter as:
X_ = PX + Qx
y = RX + Sx
Where x is the scalar input, y is the scalar output.
X is the filter state at the current time step. X_ is the updated state matrix in the n+1 time step.
P is the state transition matrix at the current time step.
Note that although I've omitted time indices, all matricies and scalars are time varying and represent a value at the current time step only. Most importantly P represents all possible state transition matrices. Laroche distinguishes them with subscript m, so P[m] is the mth state transition matrix.
It turns out that the stability analysis only needs state transition matrix P. We derive P from the scalar filter implementation given in the previous section.
For reference, our state matrix X looks like this:
| (%i22) | X: matrix([ic1eq],[ic2eq]); |

Now, to create P we extract the individual cells for the state transition matrix from the scalar filter state update expressions ic1eq_ and ic2eq_;
| (%i23) |
/* ic1eq_ = X11*ic1eq + X12*ic2eq */ X11: ratsimp(subst([ic2eq=0,v0=0],ic1eq_)/ic1eq); X12: ratsimp(subst([ic1eq=0,v0=0],ic1eq_)/ic2eq); /* ic2eq_ = X21*ic1eq + X22*ic2eq */ X21: ratsimp(subst([ic2eq=0,v0=0],ic2eq_)/ic1eq); X22: ratsimp(subst([ic1eq=0,v0=0],ic2eq_)/ic2eq); |
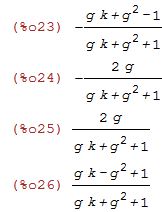
Make P. Want X_ = PX, hence the top row of P computes ic1eq_, the second row computes ic2eq_
| (%i27) | P: matrix([X11,X12],[X21,X22]); |
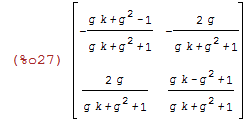
Sanity: check that P.X gives our formulas for ic1eq_ and ic2eq_ back (modulo v0 terms)
| (%i28) | P.X; |
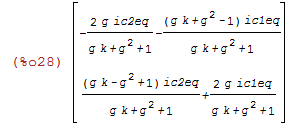
Sanity: check that (P.X - [original equations]) only has v0 terms
| (%i29) |
ratsimp((P.X)[1,1]-ic1eq_); ratsimp((P.X)[2,1]-ic2eq_); |
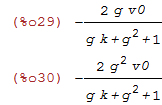
STEP 2. SHOW TIME INVARIANT STABILITY USING EIGENVALUES OF P
Eigenvalues of P are not so interesting but we can use them to sanity check time-invariant stability.
The magnitude of all eigenvalues should be less than 1 for the filter to be time-invariant stable.
This is equivalent to having the poles of the transfer function strictly inside the unit circle.
e1, e2: eigenvalues of P
| (%i31) | [e1,e2] : eigenvalues(P)[1]; |
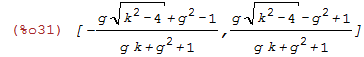
me1, me2: complex magnitude of eigenvalues e1 and e2
| (%i32) |
domain:complex; /* cabs() gives magnitude of each complex eigenvector */ [me1,me2] : cabs([e1,e2]); |
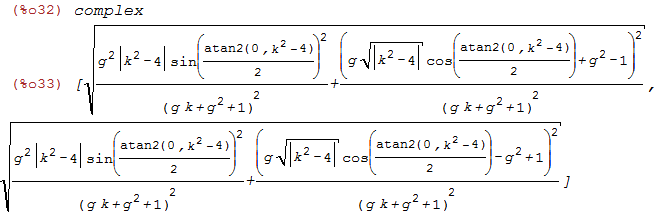
Want: |e1| < 1 and |e2| < 1
i.e. me1 < 1 and me2 < 1
| (%i34) | is(me1<1 and me2<1); |
Maxima doesn't know. Wolfram Alpha says me1 and me2 are < 1 for g>0, k>0.
[[
Here are the Wolfram Alpha queries:
sqrt((g^2*abs(k^2-4)*sin(atan2(0,k^2-4)/2)^2)/(g*k+g^2+1)^2+(g*sqrt(abs(k^2-4))*cos(atan2(0,k^2-4)/2)+g^2-1)^2/(g*k+g^2+1)^2) < 1; g>0, k>0
sqrt((g^2*abs(k^2-4)*sin(atan2(0,k^2-4)/2)^2)/(g*k+g^2+1)^2+(g*sqrt(abs(k^2-4))*cos(atan2(0,k^2-4)/2)-g^2+1)^2/(g*k+g^2+1)^2) < 1; k>0, g>0
]]
So the time-invariant filter is stable for all g>0,k>0 as expected.
+++
STEP 3. SHOW TIME-VARYING BIBO STABILITY USING LAROCHE'S CRITERIA
Laroche gives two sufficient criteria for time-varying BIBO stability. We try testing each in turn.
Laroche's Time Varying BIBO Stability Criterion 1
-------------------------------------------------
A restrictive but sufficient condition is given:
"""
If there exists a real constant 0 <= gamma < 1 such that
||P_m|| <= gamma for all m
then the corresponding time-varying filter is BIBO stable.
"""
||.|| is the induced Euclidian norm a.k.a. the Spectral Norm of matrix P (Norm[P,2] in Mathematica).
The norm can be computed as the largest singular value, or as the positive square root of the largest eigenvalue of transpose(P).P.
We use the eigenvalue method to compute the norm here.
In short, Criterion 1 requires that ||P|| < 1 for all possible transition matrices P.
Or in terms of eigenvalues of P: sqrt(max(eigenvalues(transpose(P).P))) < 1
Note that Maxima appears to be unable to solve for max() across the eigenvalue expressions so we do that step manually with the help of Wolfram Alpha.
We test Criterion 1 now.
pe1, pe2: eigenvalues of P'P
| (%i35) | [pe1,pe2] = factor(eigenvalues(transpose(P).P)[1]); |
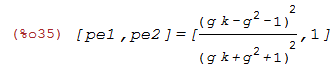
One of those eigenvalues is larger than the other.
[[
Wolfram Alpha query to show that pe1 < 1:
(g*k-g^2-1)^2/(g*k+g^2+1)^2 < 1; g>0, k>0
]]
pe1 < 1 so the norm of P is sqrt(1)=1. The norm is not strictly less than 1.
Therefore the filter does NOT fulfill Criterion 1.
+++
Laroche's Time Varying BIBO Stability Criterion 2
-------------------------------------------------
"""
If there exist a real constant 0 <= gamma < 1 and a constant nonsingular matrix T such that
||TP_mT^-1|| <= gamma for all m
then the corresponding time-varying filter is BIBO stable.
"""
According to Laroche's Criterion 2, any constant change of basis can be applied to P prior to computing the norm.
So we want: ||TPT^-1|| < 1. I'm not sure how to find a constant T that will reduce the norm of P for all k>0, g>0. It may not exist.
I guessed a T that seems to work for g>0, k>1/10000. Reduce the top left entry to lower the limit on k arbitrarily close to 1 (not proved).
T : constant non-singular change of basis matrix
Pa: P in new basis = TPT^-1
pae1, pae2: eigenvalues of Pa'Pa
| (%i36) |
T : matrix([1/10000,1],[1,0]); /* (this seems to work for k > 1/10000) */ Pa : ratsimp(T.P.invert(T)); [pae1,pae2] : factor(sqrt(eigenvalues(transpose(Pa).Pa)))[1]; |

Rather than working directly with the eigenvalues to compute the norm we can show that the largest eigenvalue < 1 using Laroche's method of inequalities on the trace and determinant of P.
In summary, (from appendix 2 in the paper) we know from Linear Algebra:
pae1+pae2=trace(Pa'Pa)=SIGMA
pae1*pae2=det(Pa'Pa)=PI
Now,
pae1<1 and pae2<1 if and only if |PI| < 1 and |SIGMA| < 1 + |PI|
Note: we show that SIGMA and PI are >= 0 as we go so as to avoid needing to take absolute values in the final inequalities.
SIGMA:
| (%i39) |
load(functs)$ /* needed for tracematrix */ SIGMA:factor(tracematrix(transpose(Pa).Pa)); |

Want: SIGMA >= 0 so we can eliminate |.| in final inequality.
SIGMA >= 0 for all g>0, k>0
True.
[[
Wolfram Alpha query:
(5000000100000000*g^2*k^2-4000000020000*g^2*k+5000000000000000*g^4+10000000400000001*g^2+5000000000000000)/(2500000000000000*(g*k+g^2+1)^2) >= 0; g>0, k>0
]]
(Note also that SIGMA blows up at k=(-g^2-1)/g. However that is outside our domain.)
PI:
| (%i41) | PI:factor(determinant(transpose(Pa).Pa)); |
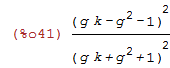
Want: PI >= 0 so we can eliminate |.| in the final inequality.
PI >= 0 for all g>0, k>0
True.
[[
Wolfram Alpha query:
(g*k-g^2-1)^2/(g*k+g^2+1)^2 >=0; g>0, k>0
]]
To meet criterion 2, we need both eigenvalues of Pa'.Pa to be < 1, which is implied by |PI| < 1 amd |SIGMA| < 1 + |PI|.
Want: |PI| < 1
Since PI >= 0 as shown above, want PI < 1
True for all g>0, k>0.
[[
Wolfram Alpha query:
(g*k-g^2-1)^2/(g*k+g^2+1)^2 < 1; g>0, k>0
]]
Want: |SIGMA| < 1 + |PI|
Since SIGMA >=0 and PI > 0
=> SIGMA < 1 + PI
=> SIGMA -1 -PI < 0
| (%i42) |
factor(SIGMA - 1 - PI); is( (SIGMA - 1 - PI) < 0 ); |
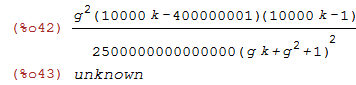
SIGMA -1 -PI < 0
True for:
g > 0, 1/10000 < k < 400000001/10000
[[
Wolfram Alpha query:
(g^2*(10000*k-400000001)*(10000*k-1))/(2500000000000000*(g*k+g^2+1)^2)<0; g>0, k>0
]]
The lower bound on k appears to be determined by the upper left entry in the change of basis matrix T. We can be moderately confident that a constant matrix T can be constructed such that Criterion 2 is met for all g>0 and for k>epsilon where epsilon is arbitrarily close to 0.
Therefore, we have shown by rough means that the transition matrix P fulfills Laroche's Criterion 2 and hence is time-varying BIBO stable.
+++
APPENDIX: SHOW THAT FILTER IS TIME-VARYING BIBO STABLE FOR UPDATE EVERY SECOND SAMPLE
This approach was tried prior to finding a workable T above and is left here for completeness only. It shows that the filter meets Criterion 1 for update every second sample.
Try looking at ||P^2|| since this would give BIBO stability changing every second sample.
This is the method that Laroche uses to prove that the Normalized ladder is stable for update every second sample. See Appendix 2 in the Laroche paper.
| (%i44) |
P; P2:P.P; eigenvalues(transpose(P2).P2); |

Using Laroche's method on determinant and trace to show that the eigenvalues of P^2 are < 1.
Rather than try to prove that the eigenvalues are < 1 directly we use Laroche's method of inequalities on the determinant and trace.
We check that SIGMA and PI are >= 0 as we go to avoid needing to take absolute values in the final inequality.
| (%i47) |
/* e1+e2=trace(P2.P2')=SIGMA */ SIGMA:factor(tracematrix(transpose(P2).P2)); |
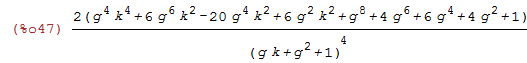
SIGMA >= 0 for g>0, k>0
True. So SIGMA = |SIGMA|
[[
Wolfram Alpha query:
(2*(g^4*k^4+6*g^6*k^2-20*g^4*k^2+6*g^2*k^2+g^8+4*g^6+6*g^4+4*g^2+1))/(g*k+g^2+1)^4>=0; g>0, k>0
]]
| (%i48) |
/* e1*e2=det(P2.P2')=PI */ PI:factor(determinant(transpose(P2).P2)); |
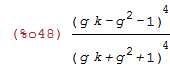
PI >= 0 for g>0, k>0
True. So PI = |PI|
[[
Wolfram Alpha query:
(g*k-g^2-1)^4/(g*k+g^2+1)^4>=0; g>0, k>0
]]
PI < 1 for all g>0, k>0
True.
[[
(g*k-g^2-1)^4/(g*k+g^2+1)^4<1; g>0, k>0
]]
Need both eigenvalues of P2.P2' to be < 1. which is implied by |PI| < 1 AND |SIGMA| < 1 + |PI|.
Want |SIGMA| < 1 + |PI|. so want |SIGMA| -1 - |PI| < 0.
| (%i49) | factor(SIGMA - 1 - PI); |
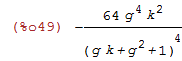
|SIGMA| -1 - |PI| < 0
True for all g>0, k>0
[[
-(64*g^4*k^2)/(g*k+g^2+1)^4 < 0; g>0, k>0
]]
Therefore the filter is time-varying BIBO stable for update every second sample.
+++