Show that we can cook up a change of basis matrix T that achieves our desired stability criteria.
| (%i1) |
/*P : matrix([a,b],[c,d]);*/ P : matrix([-(g*k+g^2-1)/(g*k+g^2+1),-(2*g)/(g*k+g^2+1)],[(2*g)/(g*k+g^2+1),(g*k-g^2+1)/(g*k+g^2+1)]); T : matrix([1,f],[0,1]); |
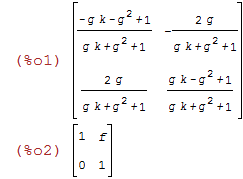
| (%i3) | ratsimp(determinant(P)); |
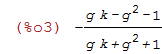
Pa is our P matrix changed using change of basis T
| (%i4) | Pa : ratsimp(T.P.invert(T)); |
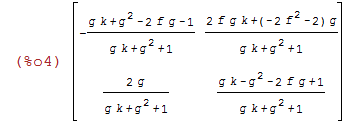
| (%i5) | ratsimp(transpose(Pa).Pa); |
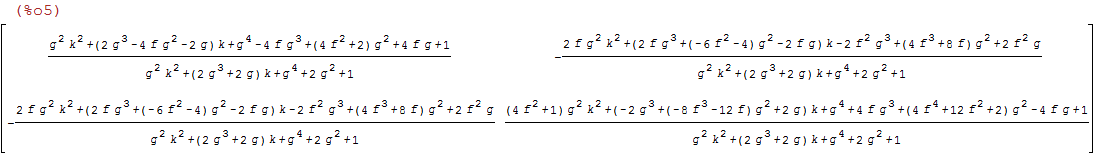
| (%i6) |
load(functs)$ /* needed for tracematrix */ SIGMA : factor(tracematrix(transpose(Pa).Pa)); |
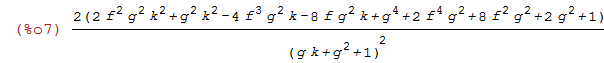
SIGMA >= 0
True
[[ (2*(2*f^2*g^2*k^2+g^2*k^2-4*f^3*g^2*k-8*f*g^2*k+g^4+2*f^4*g^2+8*f^2*g^2+2*g^2+1))/(g*k+g^2+1)^2 >= 0 ]]
| (%i8) | PI:factor(determinant(transpose(Pa).Pa)); |
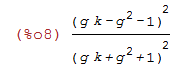
So PI = det(P)^2
| (%i9) | is(PI = ratsimp(determinant(P))^2); |
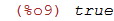
Our ||TPT^-1|| < 1 requirement is achieved by:
|PI| < 1 and |SIGMA| < 1 + |PI|
For 2x2 case:
Since PI = det(P)^2 we know it is non-negative, and SIGMA was shown non-negative above. So we have:
PI < 1 and SIGMA < 1 + PI
PI < 1
True.
[[ (g*k-g^2-1)^2/(g*k+g^2+1)^2 < 1; g>0, k>0 ]]
SIGMA < 1 + PI
=> SIGMA - 1 - PI < 0
| (%i10) | factor( SIGMA - 1 - PI ); |
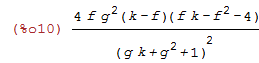
Want : SIGMA - 1 - PI < 0
[[ (4*f*g^2*(k-f)*(f*k-f^2-4))/(g*k+g^2+1)^2 < 0; 0 < k <= 2, 0
Wolfram Alpha gives solution:
0 < f < 2, g > 0, f < k <= 2